Le dipôle (R, C) 1.Lecondensateur 1.1.Constitution et symbole a. La constitution: Un condensateur est un composant électrique const...
Le dipôle (R, C)
1.Lecondensateur

1.1.Constitution et symbole
a. La constitution: Un condensateur est un composant électrique constitué de deux armatures métalliques (conducteurs) séparés par un isolant
appelé diélectrique.
Les condensateurs sont caractérisés par leurs capacité C qui s’exprime en Farad.
b. le symbole :le symbole électrique du condensateur est:
1.2.Modélisation d’un
condensateur
Orientation
symbolique d’un condensateur en
convention récepteur
La
charge q du condensateur : c’est la charge portée par l’armature vers
laquelle se dirige le sens choisi du courant en convention récepteur.
Relation
charge-intensité :
Relation
charge-tension :
Relation intensité-tension :
1.3.La capacité d’un condensateur
On
réalise le montage ci-dessous:
Le
condensateur étant initialement déchargé, on ferme l’interrupteur K à l’instant de
date t = 0.
Le condensateur se charge avec un générateur de courant continu d’intensité constante
I0 =2,0 mA.
On enregistre les valeurs de la tension
uAB aux
bornes du condensateur au cours du temps.
Le graphe obtenu montre que la tension est une fonction linéaire du temps.
On peut écrire : uAB= a.t a=50 V.s-1
Le condensateur étant initialement déchargé, on a : qA = I0 .t
On déduit des
deux relations la relation : qA = 𝑰𝟎/a ×𝒖𝑨𝑩=𝑪×𝑼𝑨𝑩
𝑪= 𝑰𝟎/a = 𝟐.𝟏𝟎−𝟑 /50= 𝟒𝟎×𝟏𝟎−𝟔 F =40 uF
2.
Réponse d’un dipôle RC à un échelon de tension
L’association
série d’un condensateur de capacité C et d’un conducteur ohmique de de
résistance R
constitue un dipôle RC
2.1. Montage expérimentale
2.2.Echelon de tension:
Un dipôle est
soumis à un échelon de tension lorsque la tension à ses bornes passe
brusquement d’une valeur constante à une autre valeur constante.
Echelon de tension
montant Echelon de
tension descendant
2.3. Charge du condensateur:Echelon de tension montant
a. Equation différentielle
b. Solution de l’équation différentielle
c. Evolution de la tension uc (t), la charge q(t) et l’intensité du courant i(t)
d.Influende de la résistance et de la
capacité.
2.4. décharge du
condensateur:
a. Equation différentielle
le condensateur préalablement chargé ,on bascule le commutateur K en position2, il se
décharge
à travers la résistance R .
b. Solution de l’équation différentielle: détermination des constantes A,B et α :
c. Evolution de la tension u c (t), la charge q(t) et l’intensité du courant i(t)
d.Influende de la résistance et de la capacité.
3.La
constante de temps: détermination graphique
3.1.La
constante de temps: Expression et unité
Le produit RC est appelé constante de temps du dipôle RC , noté ζ. Il est homogène à un temps.
Analyse
dimensionnelle:
3.2. Détermination graphique de
la constante de temps
a. Charge
du condensateur
ζ est l’abscisse du point d’intersection de l’asymptote à la courbe et de la tangente
à l’origine.(méthode de la tangente)
ζ est l’abscisse du point d’ordonné
0,63.E (méthode numérique)
b.
Décharge du
condensateur
ζ est l’abscisse du point d’intersection de l’axe de tempst de la tangente
à l’origine.(méthode de la tangente)
ζ est l’abscisse du point d’ordonné 0,37.E (méthode numérique)
3.Associations de condensateurs
3.1.Association en série
On
considère deux condensateurs de capacités respectives C1 etC2
,initialement déchargés et associés en série. Cette association est équivalente
à un condensateur unique de capacité C.
Généralisation : pour n condensateurs en série 1/Ce= 𝜮 1/Ci
3.2.Association en dérivation
On considère
deux condensateurs de capacités respectives C1 etC2
,initialement déchargés et associés en dérivation. Cette association est
équivalente à un condensateur unique de capacité C.
Généralisation : pour n condensateurs enparallèles Ce= 𝜮 Ci
4.Energie emmagasinée dans un
condensateur
Dans un condensateur de capacité C , l’énergie électrique
emmagasinée (stockée) s’exprime:
Ee=1/2.C U² = 1/2. q²/C (Ee en Joule , U en V et q en C))













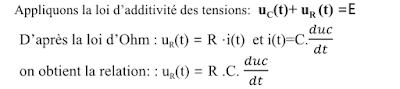
































COMMENTS