LA GRAVITATION UNIVERSELLE La Lune notre satellite naturel tourne autour de la Terre.   Quelle est la nature de la force exerce par la terr...

 LA GRAVITATION UNIVERSELLE

La Lune notre satellite naturel tourne autour de la Terre. Quelle est la nature de la force exerce par la terre sur la lune ?

I.L’échelle des longueurs de l’univers

1-Unité de longueur :
- Dans le S.I (Système International des Unités), l’unité de longueur est le mètre ; symbole m.

- On exprime souvent les longueurs avec des multiples ou des sous-multiples du mètre.

2 -Multiples et sous multiples

3- Unité astronomique et année lumière
A l'échelle astronomique, on utilise souvent les unités suivantes:
Unité astronomique : est la distance moyenne entre la terre et la lune tel que :1.U.A=1.5.10⁸km

L’année lumière : est la distance parcourue par la lumière dans le vide pendant une année avec une vitesse de 3.10⁸m /s.

4- Ecriture scientifique d'un nombre:
La notation scientifique est l’écriture d’un nombre sous la forme du produit : a.10ⁿ

Avec a : nombre décimal   a < 10 et n, entier positif ou négatif

Exemple : 452000 m=4,52.10⁵ m ; 0,002180 m=2,18.10^-3 m ; 68321 m=6,8321.10⁴m

5. L'ordre de grandeur 
a. Définition de l'ordre de grandeur
 La notation scientifique est l’écriture d’un nombre sous la forme du produit : a.10n Avec a : nombre décimal 1≤ a < 10 et n, entier positif ou négatif Si a < 5 alors l'ordre de grandeur du nombre est10n : . Si a≥ 5 alors l'ordre de grandeur est 10n+1 


b. Comparaison de deux valeurs numériques :Pour comparer les valeurs prises par une grandeur physique (Exemples : une masse une longueur) , il faut les convertir dans la même unité. Deux valeurs seront du même ordre de grandeur si le quotient de l'ordre de grandeur de la plus grande par la plus petite est compris entre 1 et 10

   6.L’échelle des longueurs:
On place sur une échelle non linéaire des objets allant de l’infiniment petit à l’infiniment grand. Pour une échelle non linéaire, la distance inter-graduation n’est pas identique d’une graduation à l’autre. Pour une échelle linéaire, la distance entre chaque graduation est identique et répétitive.
a. Soit les différentes dimensions suivantes
 

Longueur (dimension)	Ecriture scientifique	Ordre de grandeur
Distance Terre-Lune = 380 000 km	3,8.108 m	108 m
rayon atome d’hydrogène =  1,05.10-10 m	1,05.10-10 m	10-10 m
Altitude du Toubkal=4,16 Km	4,16.103 m	103m
Dimension d’une molécule = 2 nm	2.10-9 m	10-9 m
Rayon de la Terre = 6400 km	6,4.106 m	107 m
Taille d’un homme = 170 cm	1,70 m	1 m
Distance terre-Soleil = 150 million de km	1,50.1011 m	1011 m
Rayon du noyau d’un atome  d’hydrogène = 10-15 m	10-15 m	10-15 m
Diamètre de notre Galaxie = 9,5.1017 km	9,5.1020 m	1021 m
Dimension d’une cellule humaine = 10um	10-5m	10-5m
Rayon du Soleil = 700 000 km	7.108 m	109 m
Taille estimée de l’Univers = 12.1022 km	1,2.1026 m	1026 m

 b. On place chaque objet en utilisant son ordre de grandeur


II - la gravitation universelle:
1- Enoncé et l’expression mathématique de la loi de Newton de la gravitation universelle
1-1- Enoncé de la loi :
A cause de leurs masses, les corps exercent mutuellement les uns sur les autres des forces à effets attractifs.
1-2- L’expression mathématique de la loi de Newton :
Deux corps A et B ponctuels (c'est-à-dire de petite dimension par rapport à la distance qui les sépare), de masses respectives  et  , séparés d’une distance d , exercent l’un sur l’autre des forces d’attractions gravitationnelle .

 : la force exercée par le corps A sur le corps B

 : la force exercée par le corps B sur le corps A

Les caractéristiques de la force d’interaction gravitationnelle sont les suivantes :

Direction : la droite joignant les centres de A et B ;

Sens : orienté vers le corps qui exerce la force ;

Intensité : 

MA et MB : masses des corps A et B exprimées en kilogramme (Kg) .

 d : la distance entre les deux corps en mètre (m)  .

 G: la constante de gravitation universelle dont la valeur est : G=6,67×10⁻¹¹ (S.I)

 FA et FB : intensités des forces exprimées en Newton (N)

2- L’interaction gravitationnelle entre 2 corps à répartition sphérique de masse

La loi de l’attraction gravitationnelle peut être généralisée à tous les corps à répartition sphérique de masse. Un corps à répartition sphérique de masse est un corps dont la matière est répartie uniformément autour de lui ou en couches sphériques homogènes autour de son centre. c’est le cas de la Terre, de la Lune, des Planètes et des Etoiles.

III –Poids d’un corps et force gravitationnelle

    1- Poids d’un corps
En absence du mouvement de rotation de la terre autour de l’axe passant par ses pôles. Le poids d’un corps est la force d’attraction qu’il subit lorsqu’il est situé à la surface de la Terre ou, à proximité de sa surface. Le poids d’un corps est essentiellement la force de gravitation que la Terre exerce sur lui.

   2- Caractéristiques du poids
Les caractéristiques du poids sont :
- Point d’action : centre de gravité du corps.  
- ligne d'action : la verticale passant par G.
- sens : de haut en bas (vers le centre de la Terre).
- intensité (ou valeur) : P = m. g
   3-Expression de l’intensité de la pesanteur

Le poids P d’un corps situé à l’altitude h de la surface de la Terre, peut-être identifié à la force de gravitation F exercée par la Terre sur ce corps :

Corps à la surface de la terre: 

Corps à l'altitude h de la surface de la terre:

g_h : intensité de pesanteur a l’altitude h, en N.kg^-1
g₀ : intensité de pesanteur a la surface de la terre (h=0), en N.kg^-1

4-Relation entre g₀ et g_h
des deux relations précédentes (1) et (2)  :

Exercices

Exercice1:

1)- Donner l’expression littérale de la valeur de la force d’attraction gravitationnelle exercée par le Soleil sur la Terre.

2)- Calculer la valeur de cette force.

3) Représenter cette force, sur le schéma ci-dessous en utilisant l'échelle 1cm→10²²N

Données :
G = 6,67 x 10⁻¹¹ m ². kg⁻² . N
g = 9,8 N / kg
Masse de la Terre : m т = 5,98 x 10 ²⁴ kg
Masse du Soleil : m s = 2,0 x 10 ³ºkg
Distance Terre- Soleil (entre les centres) d TS = 1,50 x 10 ¹¹ m

Correction de l'exercice1

1) Expression littérale de la valeur de la force d’attraction gravitationnelle exercée par le Soleil sur la Terre:

-

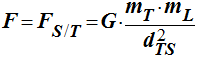
2)Valeur de cette force F:

 

3) Représentation de la force exercée par le soleil sur la terre:

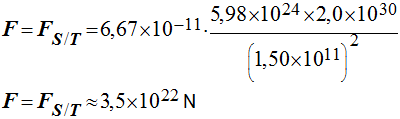
Exercice2 :

Énoncé :

Un satellite artificiel de masse 1,80 x 10 ³ kg tourne autour de la Terre, sur une orbite circulaire, à une altitude de 250 km.

1)- Donner l’expression de la valeur de la force d’attraction gravitationnelle exercée par la Terre sur le satellite. Calculer sa valeur.

2)- Représenter cette force sur le schéma (ci-dessous) faisant apparaître la Terre et le satellite en utilisant l’échelle suivante : 1 cm pour 10 ⁴ N.

3)- Le satellite exerce une force sur la Terre. La comparer à celle exercée par la Terre sur le satellite.

Données : G = 6,67 x 10 – 11 m 2 . kg– 2 . N Masse de la Terre : m T = 5,98 x 10 24 kg Rayon de la Terre: R T = 6378 km

Correction de l'exercice2

1)

 Expression littérale de la force F: 

Valeur de la force F :

   F ≈ 1,63 x 10 ⁴ N

2)- Représentation du vecteur force  :

Caractéristique du vecteur force	Point d’application : O’
	Direction : la droite (OO’)
	Sens : de O’ vers O
	Valeur de la force :  F ≈ 1,63 x 10 4 N Longueur de la flèche : ℓ F ≈ 1,63 cm

3) Les deux forces ont meme direction , meme valeur, mais de sens opposées

Exercice3 :

1. Quelle est la valeur P du poids d'une boule de masse m = 800 g , posée sur le sol ?

2. Quelle est la valeur de la force gravitationnelle F exercée par la Terre sur la même boule ?

3.  Comparer ces deux forces et conclure.

4.  En déduire l'expression de l'intensité de la pesanteur g en fonction de G, M_Tet R_T.

Données : g = 9,8 N kg -' ; rayon de la Terre R_T = 6380 km ; masse de la Terre

M_T = 5,98 . 10²⁴kg

Correction de l'exercice3

1. P=m×g= 0,8 ×9,8=7,84N

2. 

3. On constate que le poids de la boule (

P$$P$$) et la force gravitationnelle exercée par la Terre sur la boule (F$$F$$) sont égales:P=F